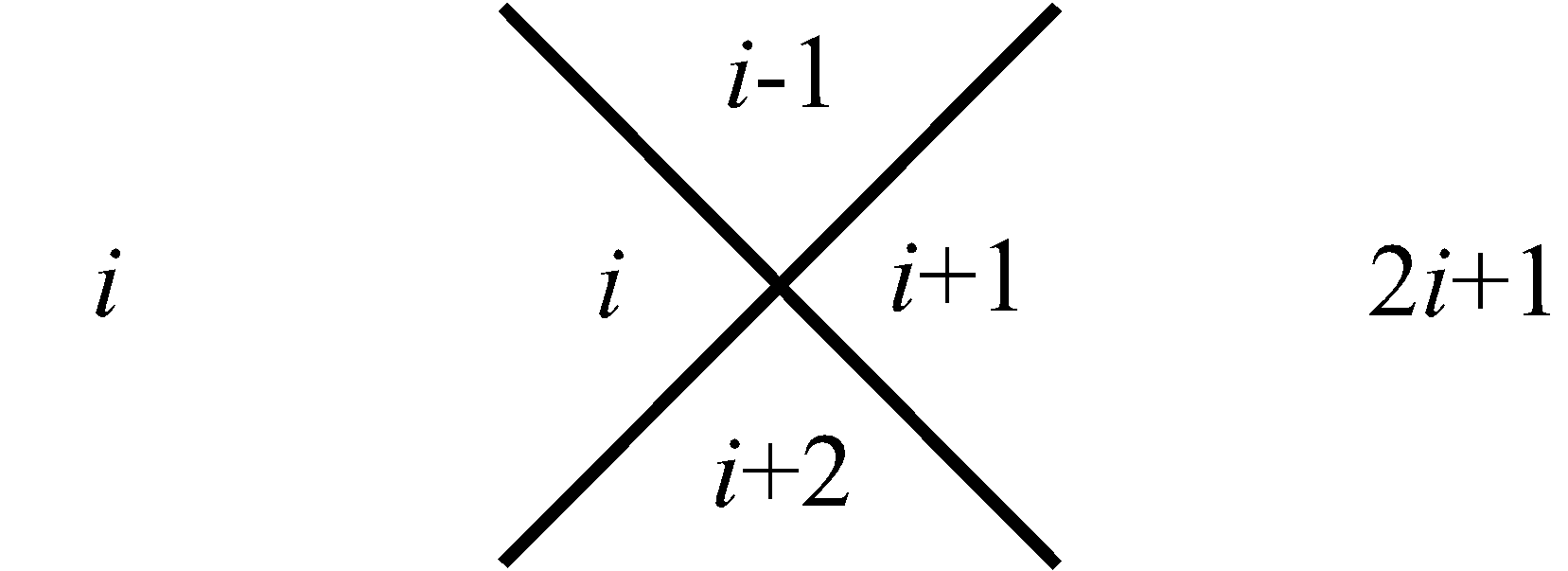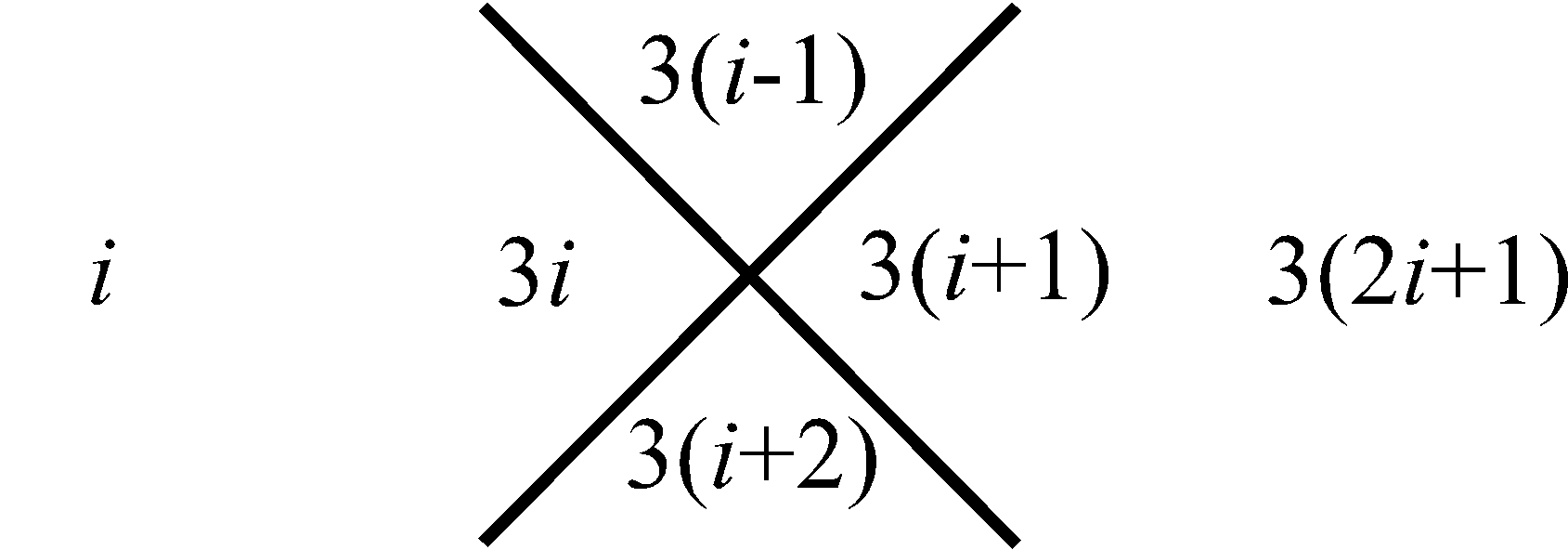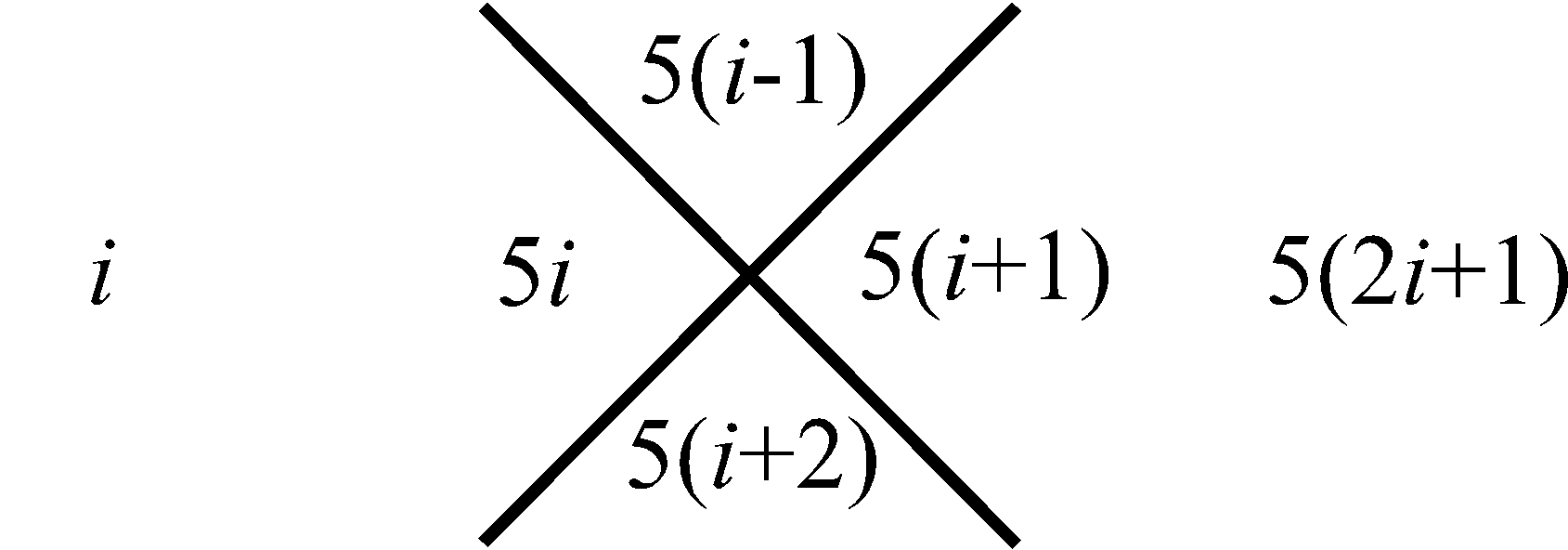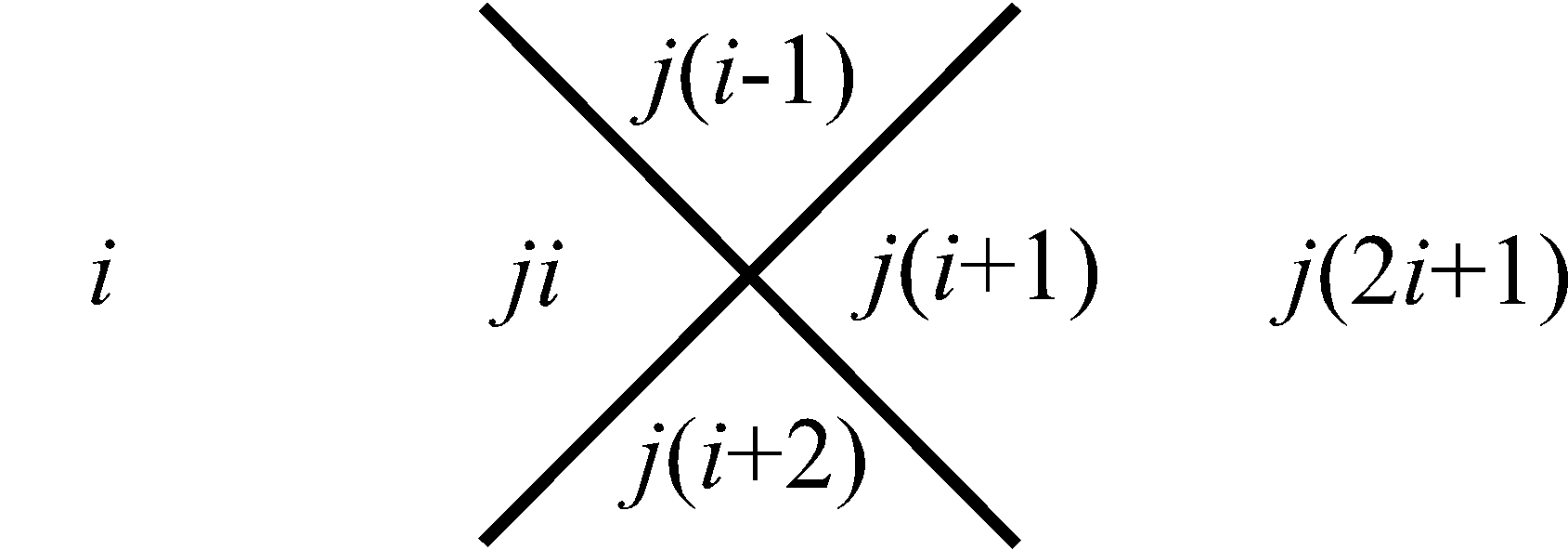ОБ ОДНОМ АЛГОРИТМЕ СТРУКТУРИРОВАНИЯ НАТУРАЛЬНОГО РЯДА ЦЕЛЫХ ЧИСЕЛ

В.А. ВЫШИНСКИЙ

Институт кибернетики им. В.М.Глушкова НАН Украины

М.Л.ТЕРЕНТЬЕВ

Детская инженерная академия. Вальдорфские классы "Борисфен", Киев

ОБ ОДНОМ АЛГОРИТМЕ СТРУКТУРИРОВАНИЯ НАТУРАЛЬНОГО РЯДА ЦЕЛЫХ ЧИСЕЛ

1. Введение

Известно, что развитие математики берет свое начало со времен осознания человеком понимания целого натурального числа, которое связывают еще со счетом – одним из первых вариантов абстрактного мышления. Именно пересчет идентичных неоднородностей распределения материи, окружающих нас, позволил структурировать множество этих чисел как совокупность, названной, со временем, рядом целых натуральных чисел. Исследователей, всегда, интересовала структура этого ряда. Например, и сегодня является актуальным установления закона распределения в нем простых чисел, а также построение алгоритма их  нахождения с так называемой полиномиальной сложностью. И эта задача стоит в рамках не простого любопытства, а ее решение, крайне нужное, в криптографии. Аналогичная задача, в свое время, стояла перед математиками в познании структуры распределения остатков целых натуральных чисел от деления на заранее заданное число [1], в последствии названное модулем, а соответствующий аппарат в математике – теорией сравнений. Первое применение такой структуры позволило организовать контроль вычислений в сложных формулах над целыми много разрядными числами, как известно, в качестве подработки, которой нагружали себя математики. В частности было замечено, что значение минимального остатка от деления целых натуральных чисел на число (модуль) 3 в их ряду повторяется. Например,

ряд натуральных чисел                            –  1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, · · ·,

минимальный остаток от деления на З –   1, 2, 0, 1, 2, 0, 1, 2, 0,  1,   2,   0,   1,    2, · · ·.

Здесь под каждым целым натуральным числом в нижнем ряду расположен  его минимальный остаток от деления на модуль 3. Было замечено, что остаток  результата вычислений по модулю 3 согласно формуле, над которой работал математик,  совпадает с остатком по модулю 3 результата вычислений по той же формуле, но с исходными данными (не полноценными многоразрядными числами), а, только, с их минимальными остатками от деления на модуль 3. В этом случае все аддитивные и мультипликативные  операции выполняются по модулю 3, т.е. после выполнения операций над исходными данными (остатками) их результат делится на 3, и при этом определяется минимальный остаток от этого деления. Это свойство равенства остатков от деления полноценного результата вычислений и вычислений по модулю было использовано для контроля вычислений, которые математику приходилось выполнять вручную. Ведь известно, что человеку присуще ошибаться, и особенно при выполнении арифметических действий над много разрядными числами. Приведенное выше свойство контроля характерно по любому модулю, однако, математики в своих вычислениях выбрали число 3. Дело в том, что это число, как и число 9, в качестве делителя степеней основания десятичной позиционной системы счисления, имеет остаток от деления равный единице, что существенно упрощает нахождение минимального остатка на указанные модули много разрядного десятичного числа. Просто, в этом случае, поиск нужного остатка сводится к суммированию цифр десятичного представления исходного числа и, затем из полученной суммы определяется минимальный остаток от деления на модуль 3.

Уже в двадцатом столетии удалось обнаружить, что на рассмотренном принципе задания числа остатками от деления на модули, можно построить систему счисления представления чисел [2]. Используя эту систему вначале семидесятых годов в Зеленограде под Москвой, была построена и довольно хорошо работала единственная в мире вычислительная машина, в которой обработка числовой информации организована в рассматриваемых остатках, т.е. в системе счисления остаточных классов. Ее авторы  И.Я Акушский и Д.И. Юдицкий перед этим (1968 год) издали книгу «Машинная арифметика в остаточных классах» [3].

В настоящей работе попытаемся исследовать также еще и другие структуры натурального ряда, представляющие интерес для понимания распределения в нем простых чисел.

2. Нетрадиционный  алгоритм над целыми числами натурального ряда

История обращения с целыми натуральными числами, как уже отмечалось, ведет в прошлое нашей цивилизации. Обратим внимание на то, что целые числа составляют множество, которое нашло свое структурирование в процессе его познания. Напомним, этому способствовала жизненная потребность пересчета чего-либо, что окружало человека, и что, в конечном итоге, позволило увидеть натуральные числа, их структуру, в виде ряда.   В дальнейшем стали отталкиваться от этого ряда, представляющего собой последовательность, получаемую на основе арифметической прогрессии, в которой в качестве ее разности выступает единица. В результате, из этого ряда выпали такие  числовые понятия, как нуль и отрицательные целые числа. В тоже время они, имеющие непосредственное отношение к процедуре счета, характеризуют свойства целых чисел. Так, понятие нуля, наряду с единицей, или пятеркой отображают ту числовую информацию, которой заинтересовался человек, исследуя окружающую среду. Если в среде пять предметов, то в натуральном ряду этому соответствует число пять, а если предметы отсутствуют, то тогда такое состояние в природе в числовом ряду изображается числовым символом нуль. Ту же самую особенность, можно заметить и на пересчете предметов, которые в данном окружении ранее были,  а на данный момент их нет.  Их удобно в математике обозначать отрицательными числами. Таким образом, к натуральному ряду чисел, полноправно, относят и нуль, и числа с отрицательным знаком [4].

Приведенное выше, понимание целых натуральных чисел позволяет их совокупность рассматривать, не обязательно в виде упорядоченного ряда, а как множество элементов аддитивной группы, и одновременно с этим, как мультипликативной  полугруппы. Иными словами множество целых натуральных чисел представляет собой кольцо. Оперированию с целыми числами, без учета их структуры в виде ряда, широко применяется в теории чисел в ее разделе, где изучаются магические квадраты. При составлении такого квадрата число, прежде всего, рассматривается как элемент множества, над которым задана аддитивная операция.

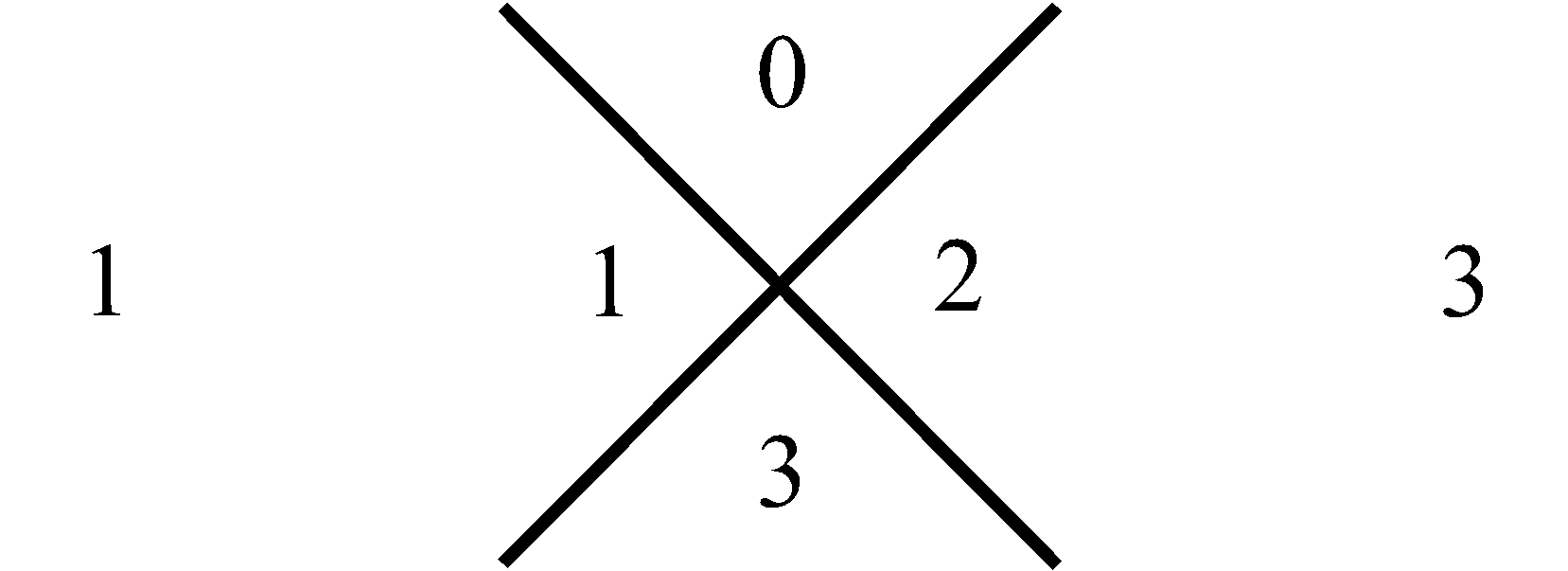
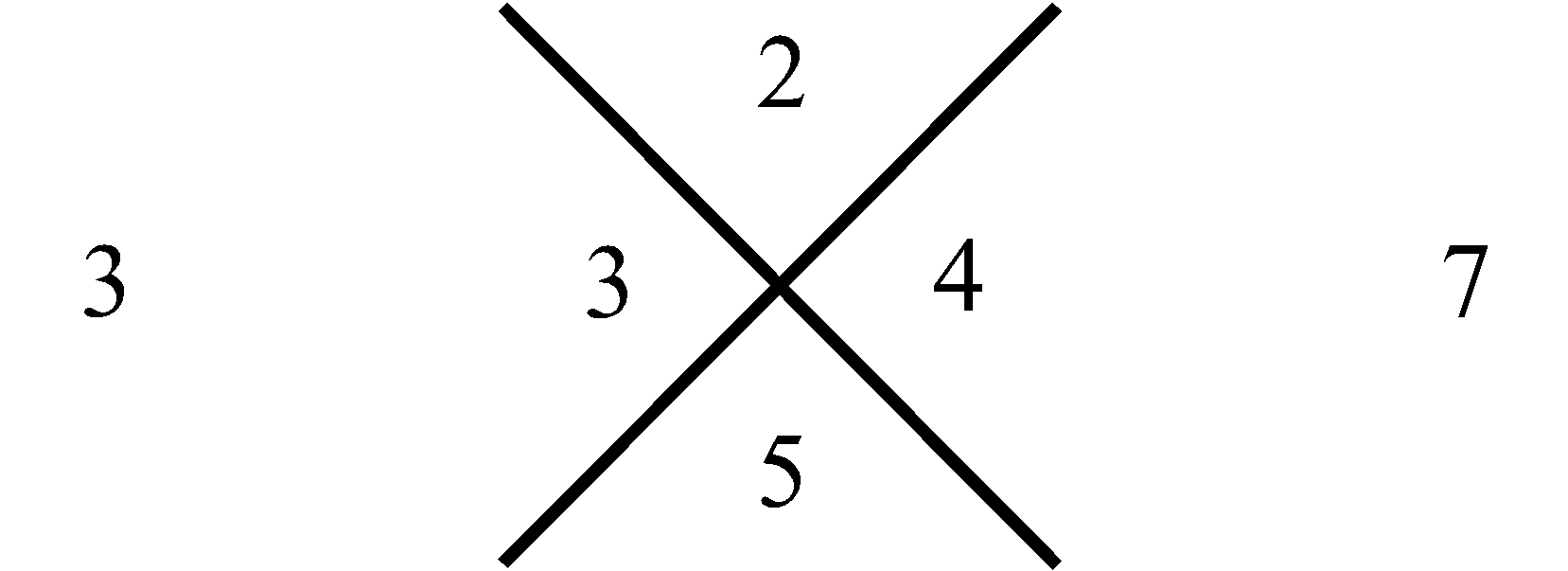
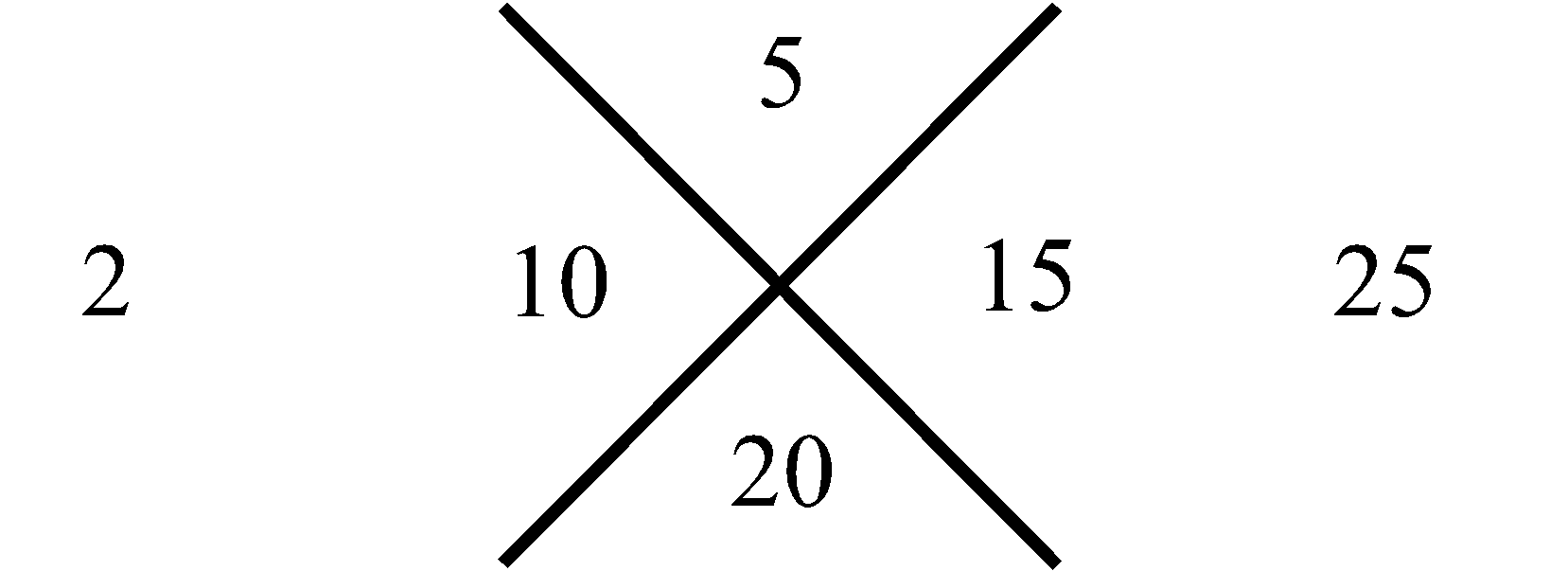
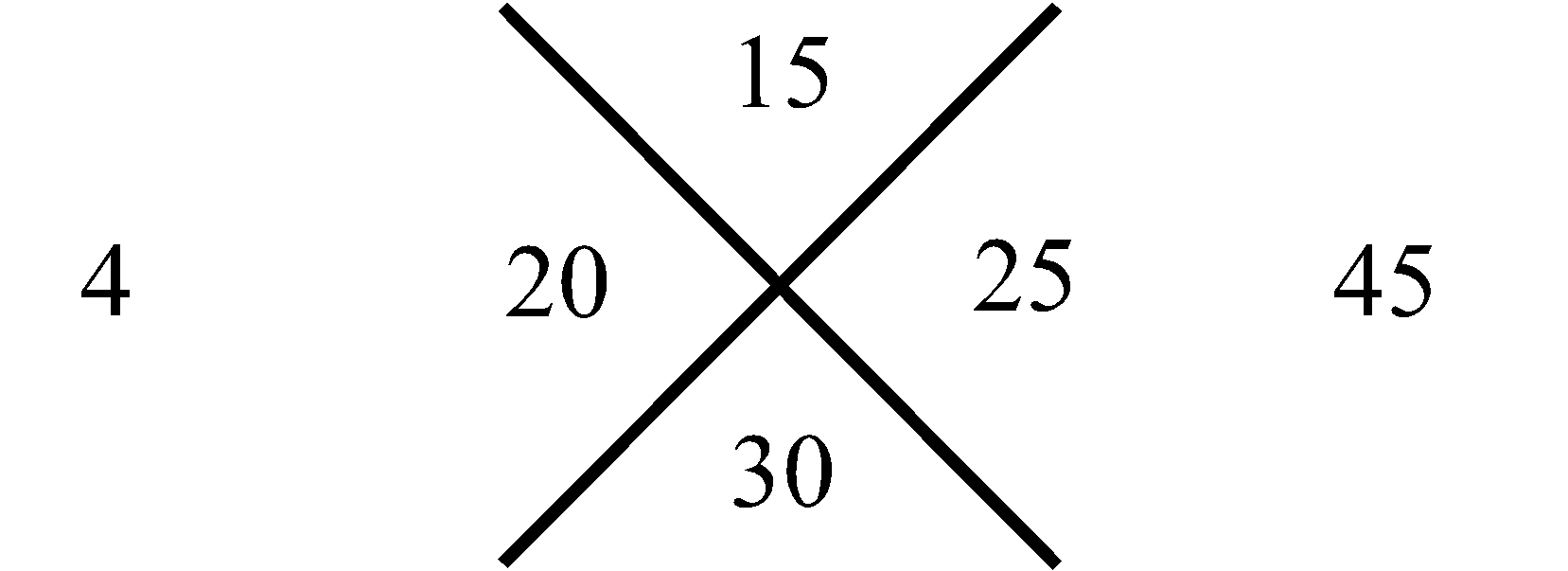
То, что натуральный ряд целых чисел представляет собой  аддитивную группу, позволяет нам использовать нуль, в качестве целого натурального числа в описании следующего алгоритма. Рассмотрим совокупности четырех целых чисел, разделенных между собой пересекаемыми прямолинейными отрезками, которые на Рис.1 расположены в виде столбца. Обратим внимание на следующую закономерность целых чисел в этих совокупностях.  Так в первой из них, вверху столбца, целые числа натурального ряда, начиная с нуля, находятся по своим секторам, которые образуются от пересечения прямолинейных отрезков. Нуль располагается в самом верхнем секторе, а единица в следующем за ним секторе, и расположенном слева от него. Затем целое число ряда два находится в противоположном секторе от того, в котором расположена единица. И, наконец, четвертое число три в самом нижнем секторе рассматриваемой совокупности чисел, т.е., если учесть последовательность секторов  в том чередовании, которая рассмотрена выше, то первые четыре целых числа натурального ряда в первой совокупности их столбца будут располагаться друг за другом. Аналогичным образом числа натурального ряда будут располагаться в следующей второй нижней совокупности столбца, только уже, начиная с единицы, как бы натуральный ряд чисел сдвинут на одну свою позицию. И таким образом со сдвигом на одну позицию натуральный ряд представлен в следующей третьей совокупности, рассматриваемого столбца.

Учитывая бесконечность ряда натуральных чисел, наш столбец совокупностей целых чисел тоже будет   бесконечным.    Миша Терентьев ученик первого класса,      соавтор    настоящей статьи, которому не было еще и восьми лет, поделился следующей особенностью рассматриваемого столбца. Он обратил внимание на то, что сумма чисел, находящихся в противоположных секторах каждой в отдельности совокупности равна одному и тому же числу. Например, для самой верхней совокупности эта сумма равна

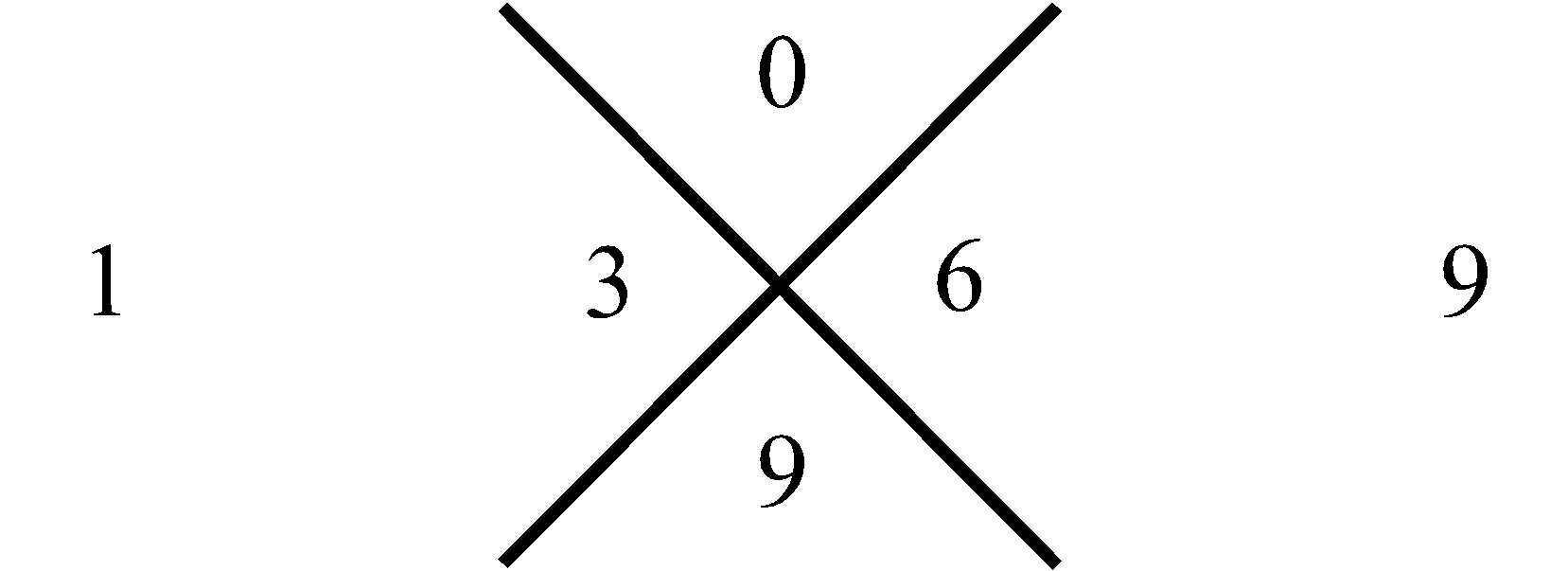
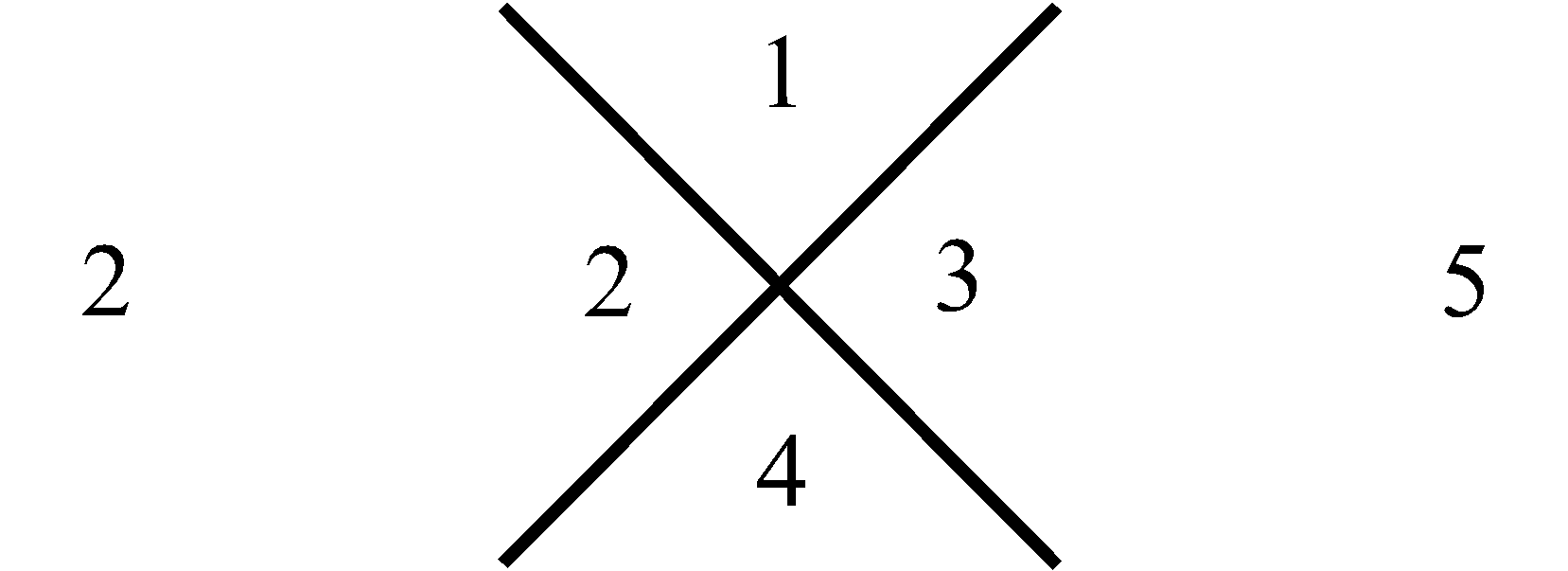
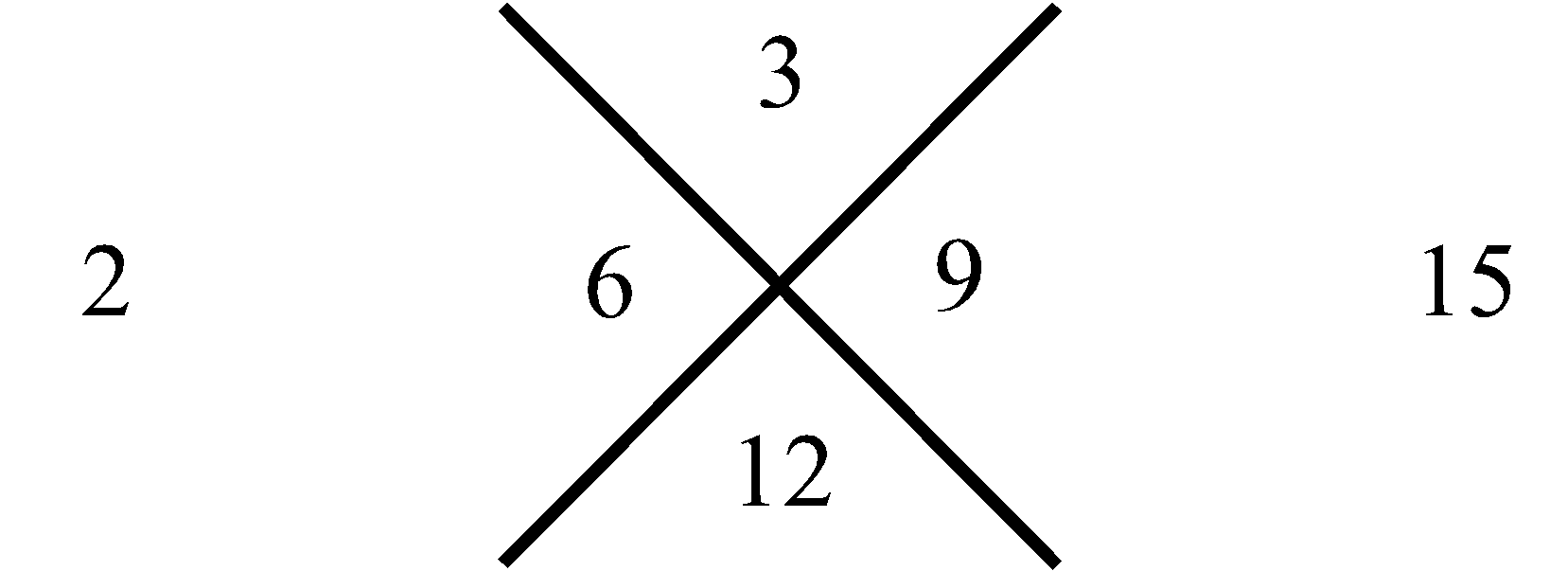
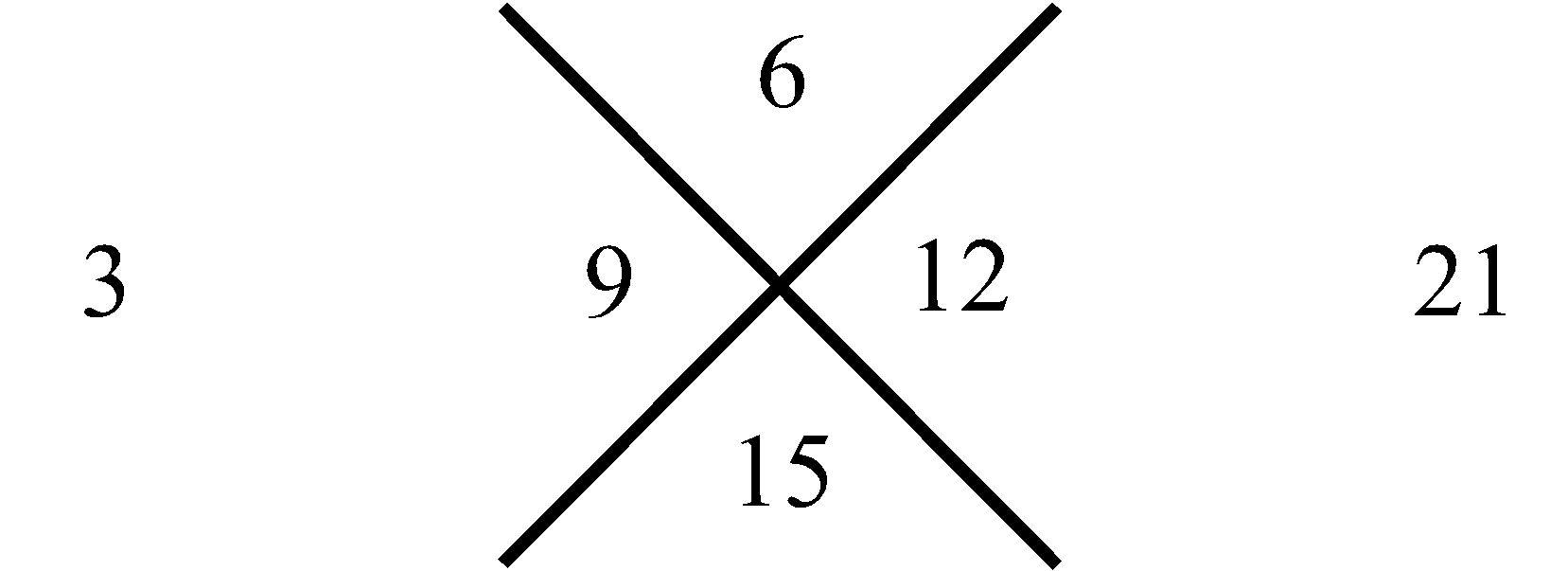
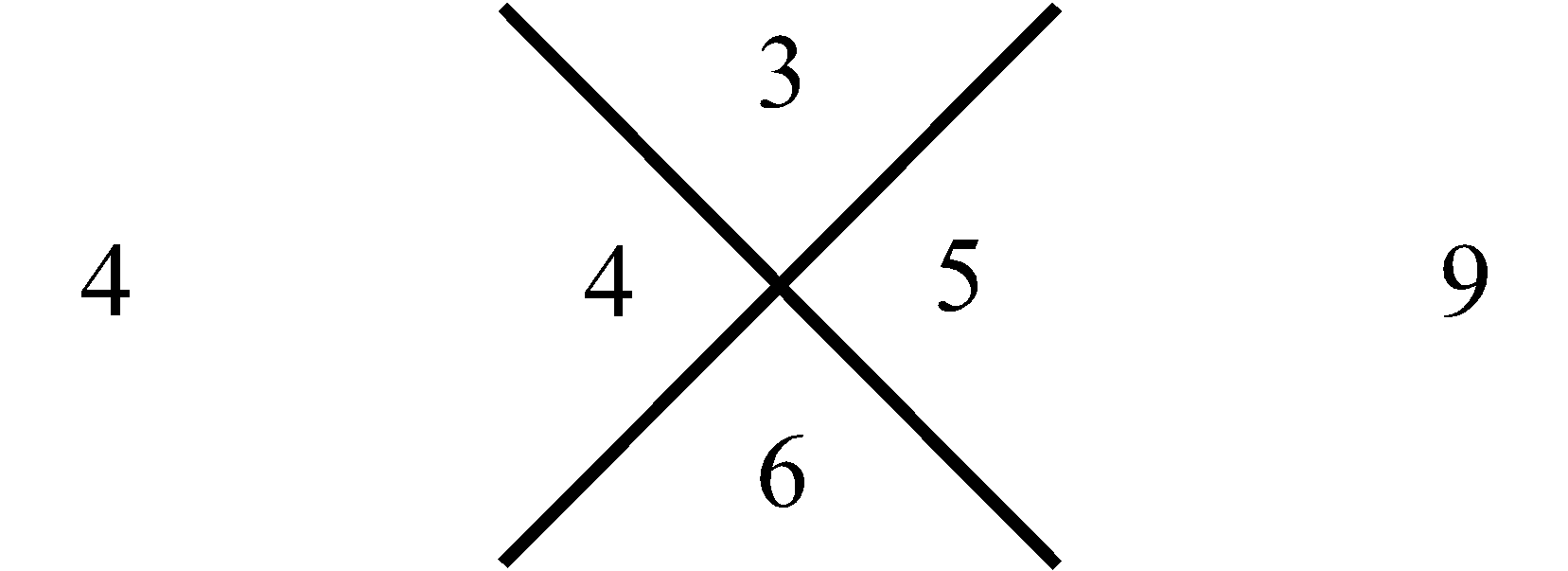
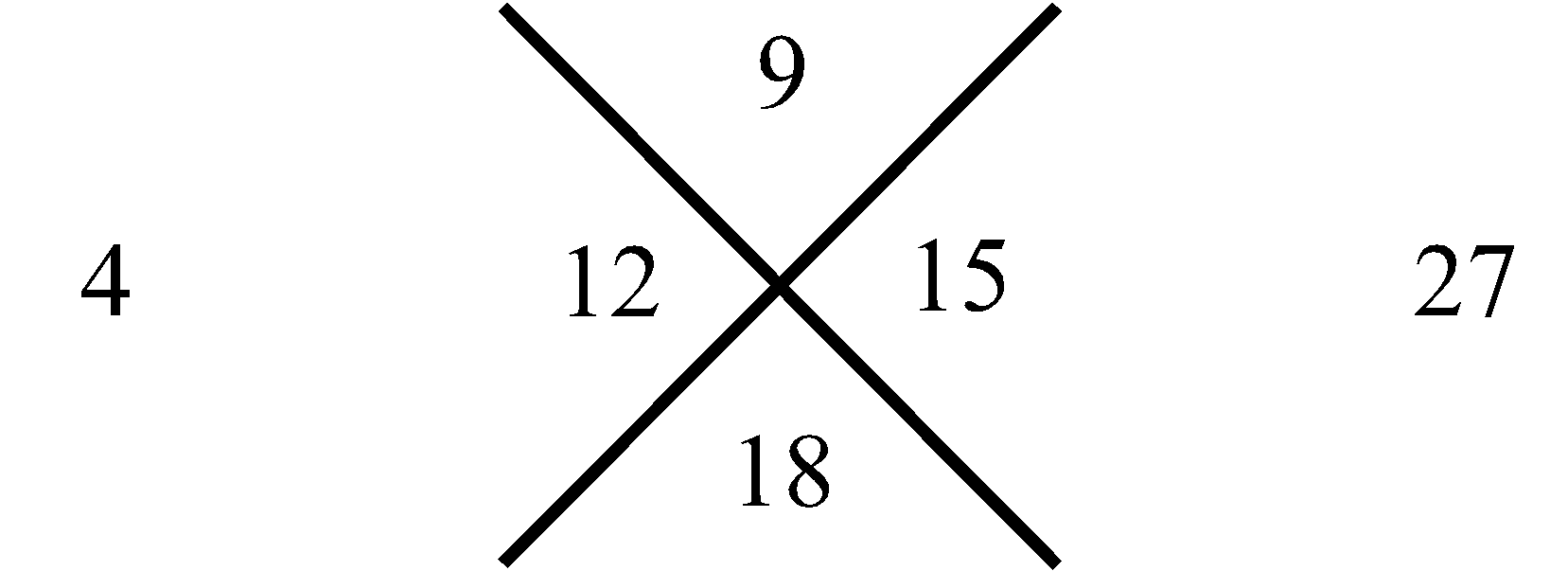
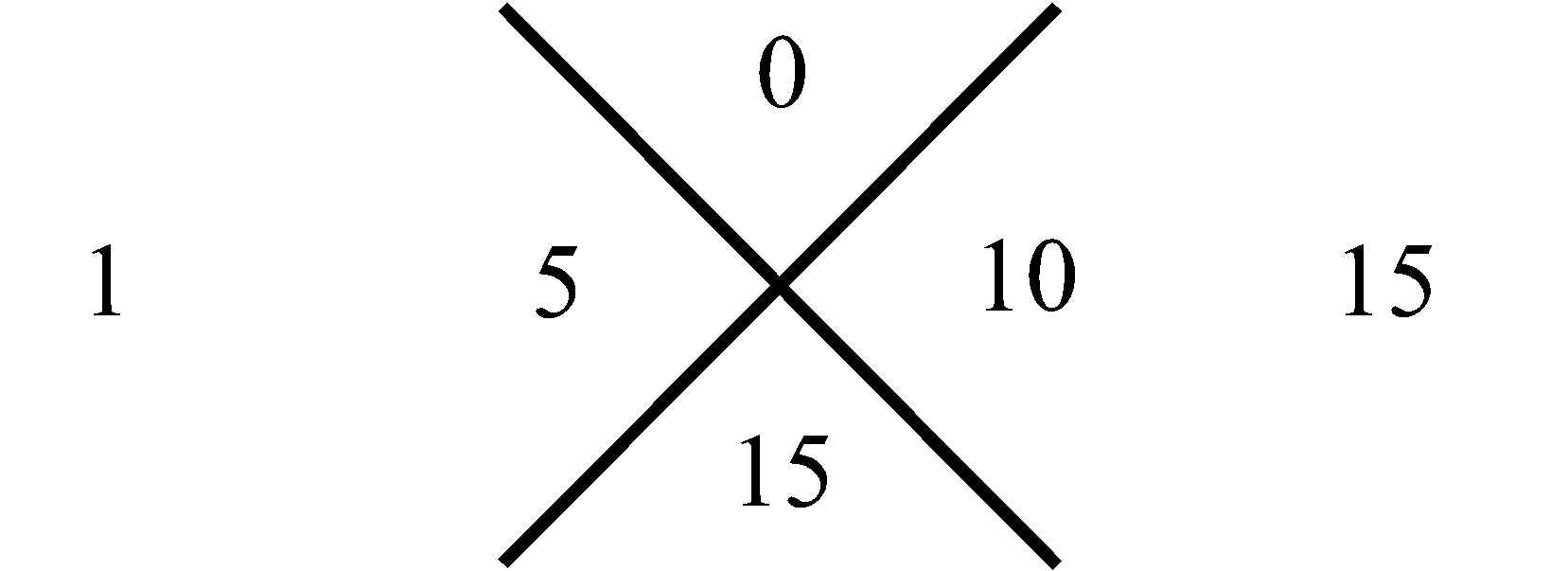
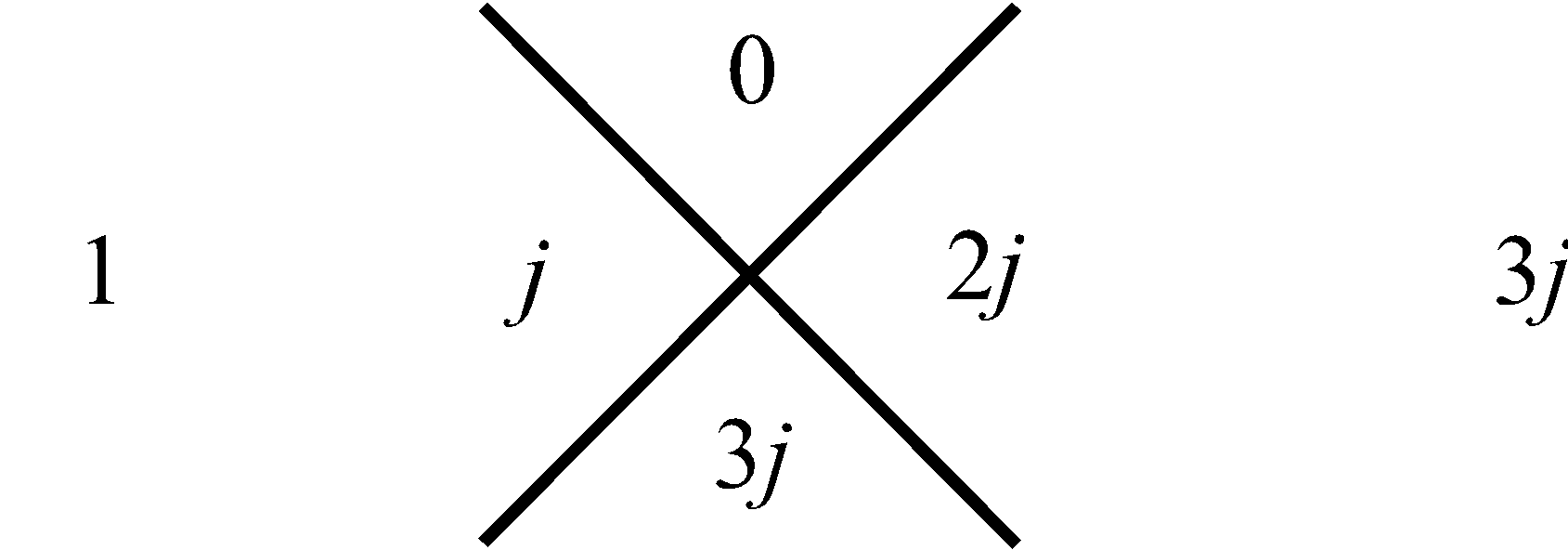
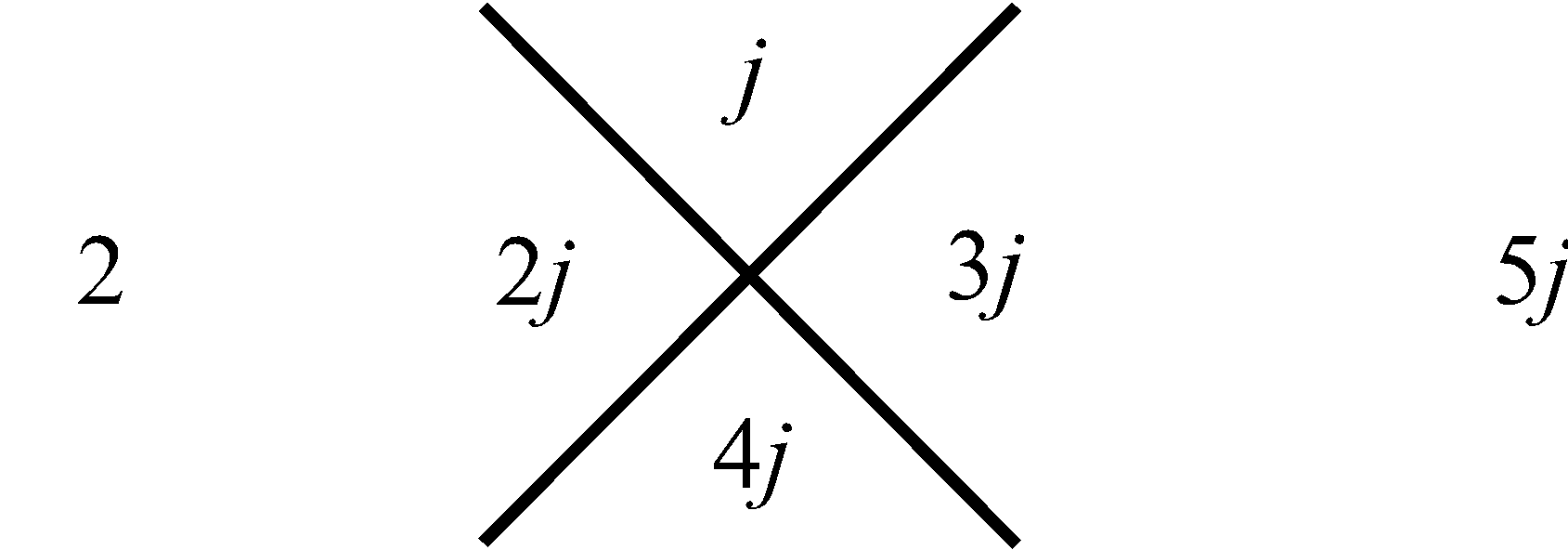
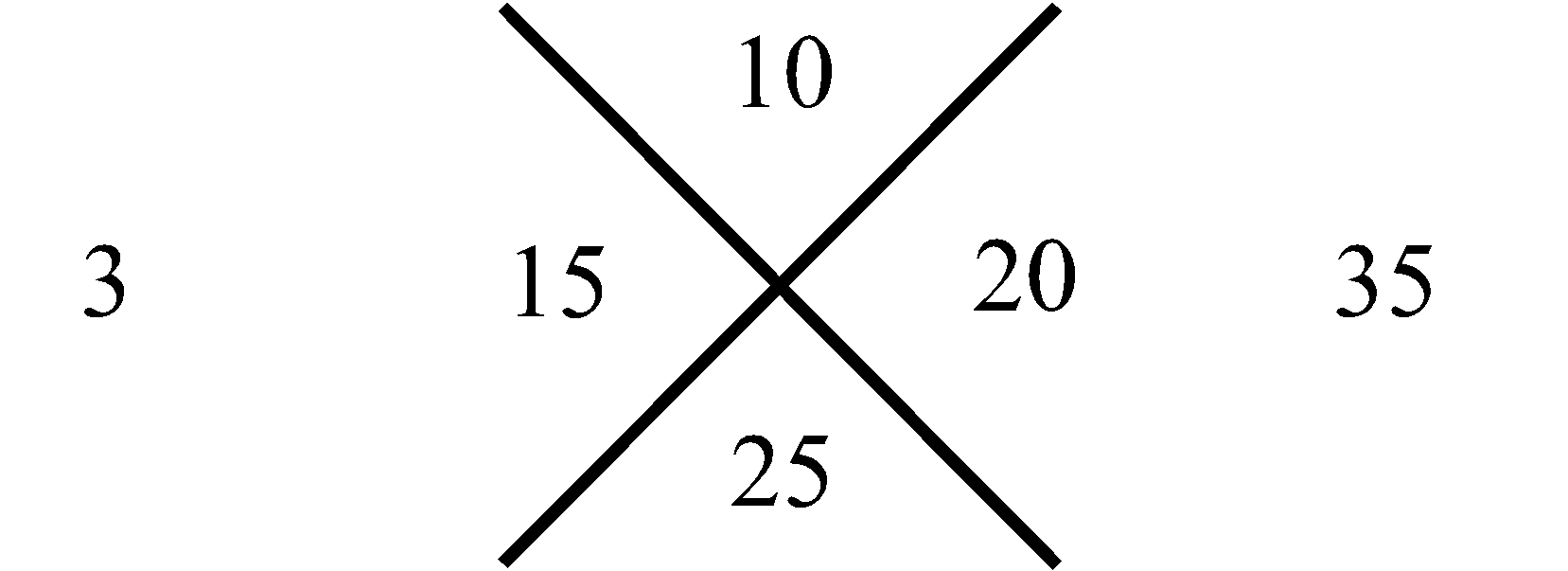
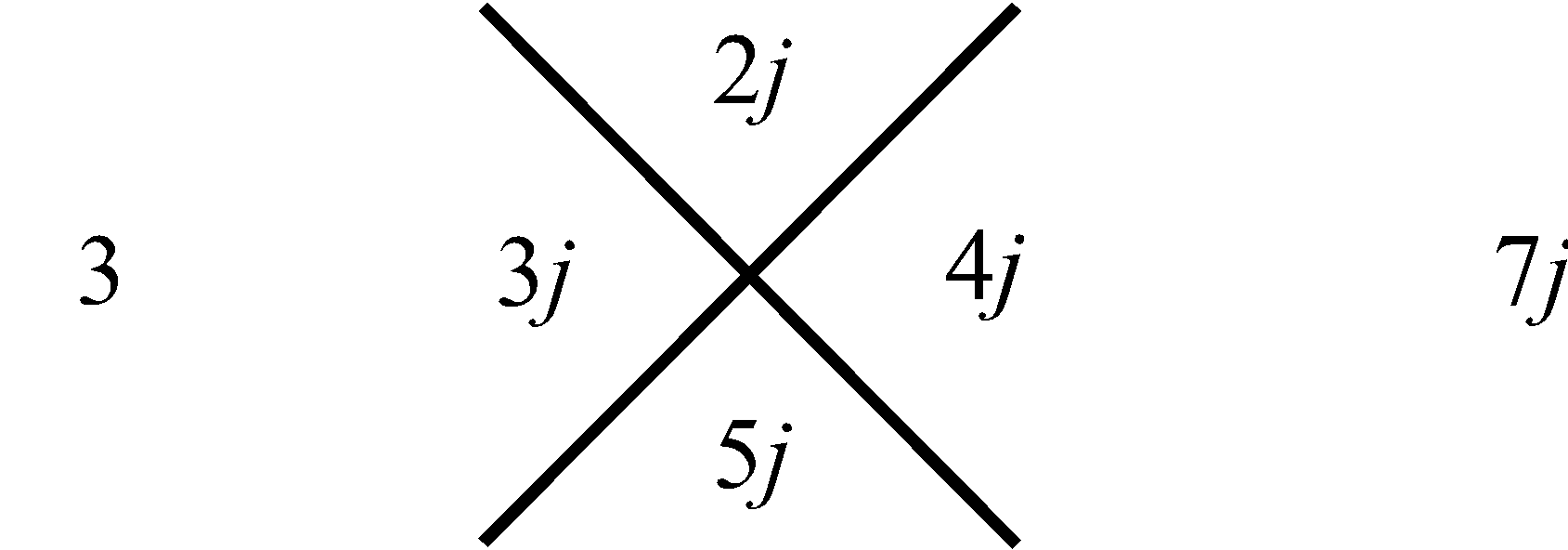
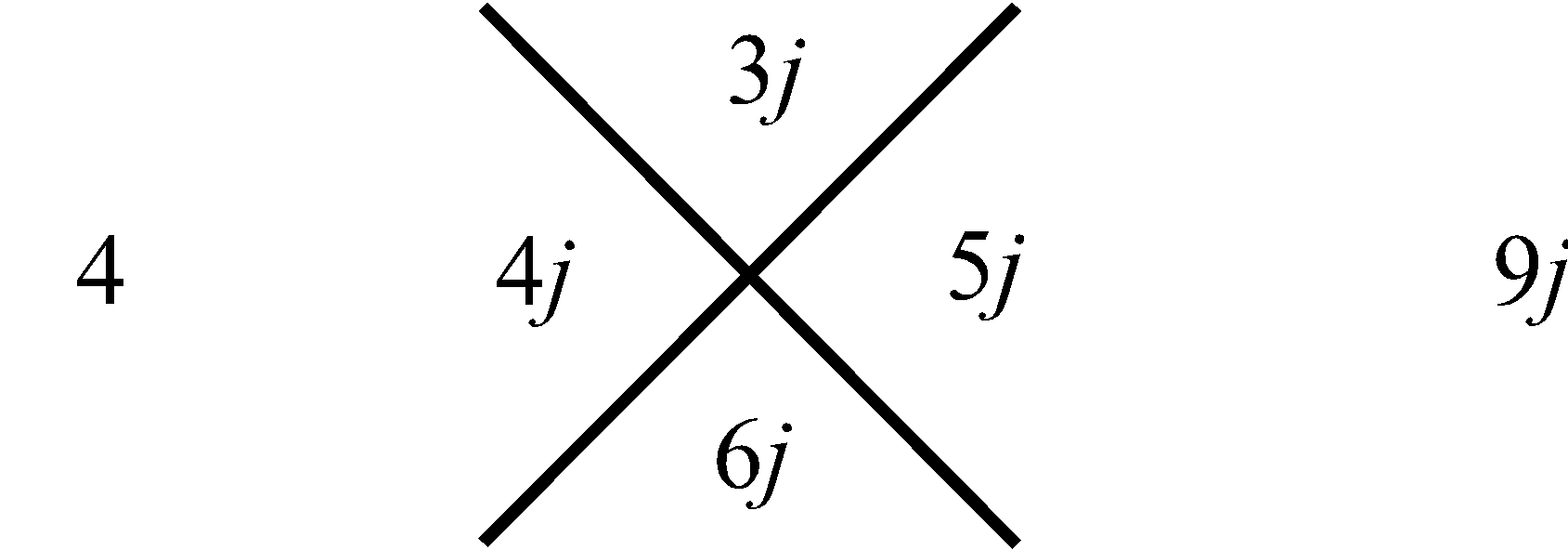
трем. Для следующей (второй) за ней совокупности, внизу, – пяти. Затем в еще нижней совокупности – семи, и так далее. Последовательность этих сумм, вдоль, рассматриваемого столбца совокупностей чисел, отображает нечетные натуральные числа в их естественной возрастающей последовательности, которая на Рис.1 представлена в столбце справа. Что касается левого столбца, то его цифры отображают перечисление совокупностей чисел в нашем столбце от 1 до бесконечности. Используем, замеченную Мишей особенность совокупностей в столбце, представленном на Рис.1, для манипуляции с простыми числами следующим образом. Построим последовательность чисел согласно арифметической прогрессии, в которой разность будет не единица, как это имеет место для натурального ряда, а первое простое число три, то тогда этой последовательности, используя прием построения столбца (Рис.1), будет соответствовать столбец, приведенный на Рис.2. На нем, справа от рассматриваемого нами столбца совокупностей чисел, расположен столбец, всех нечетных чисел (ряд, выстроенный по возрастающей их величине), которые делятся на простое число три.   На Рис.3 представлен, аналогичный столбец, из которого формируется последовательность нечетных чисел, делящихся, уже на следующее простое число пять. На   Рис.4  отображен столбец, построенный рассматриваемым приемом формирования последовательностей, каждая из которых представляет нечетные числа, делящиеся на соответствующее простое число. Совокупность столбцов изображенных на Рис.2, Рис.3 и в общем виде на Рис.4 отражают бесконечную последовательность, в соответствии с бесконечной последовательностью простых чисел. Индексы i и j принимают значение 1, 2, 3, · · · и так до бесконечности.

Если из ряда нечетных чисел (Рис.1) удалить числа кратные простому числу три, а затем, аналогичным образом, из того же ряда удалить нечетные кратные числа простому числу пять ряда и т.д., то будет формироваться новый ряд нечетных чисел, для которого имеет место следующая теорема.

Теорема.

В ряду нечетных натуральных чисел, упорядоченных согласно возрастанию их величин, и в котором удалены кратные первым n простым числам, следующее нечетное число совпадает с n+1 простым числом.

Доказательство этой теоремы проведем от противного. Допустим, что n+1 число составное, а это означает, что оно имеет делители, естественно, меньшие по величине, нежели оно само.  Тогда такими делителями могут быть только простые числа. Однако составные числа с такими делителями уже изъяты из рассматриваемого ряда нечетных чисел, из чего следует, что рассматриваемое число принадлежит ряду простых за номером n+1.

3. Выводы

Итак, рассмотрен алгоритм, позволяющий выделить во множестве целых натуральных чисел его структуры в виде рядов нечетных составных чисел. Преимущество этого алгоритма состоит в том, что он содержит в себе только аддитивные операции (сложение простых чисел и операции сравнения), т.е. он существенно проще известных алгоритмов, которые основаны на реализации мультипликативных операций (умножение и деление чисел). Это преимущество, особенно, проявляется при организации вычислительного процесса на средствах обработки информации над числами с большой разрядностью, которые участвуют в алгоритме. Отмеченное упрощение весьма важно для алгоритма поиска в натуральном ряду простых чисел, особенности которого будут рассмотрены в отдельной работе.

Литература

1. Гаусс К.Ф. Труды по теории чисел / К.Ф.Гаусс // Издательство АН СССР, 1959. – 967 с.

2. Svoboda A. Rational numerical System of residual classes/ A. Svoboda // Storog na zpacovani informaci, sbornik V, Nak 1 CSAV, 1957.

3. Акушский И.Я., Юдицкий Д.И. Машинная арифметика / И.Я.Акушский, Д.И.Юдицкий // Изд. «Советское радио» Москва – 1968 438с.

4. Виноградов И.М. Основы теории чисел / И.М.Виноградов // М: Наука, 1972 – 178 с.